This week I am cutting to the chase! No long jargon-laden intros, no musings about jargon—now it’s all about the trees, baby! In fact, it’s all misconceptions about trees, and we’re going to tackle three of them.
Misconception number one, come on down!
Misconception: Evolutionary trees have “main lines” of evolution and “side tracks” of evolution.
Correction: There are no “main lines” or “side tracks” in evolution or (consequently) in evolutionary trees.
It might seem intuitive that the lineage from the root to the furthest branch tip represents the main artery of evolution, and all other paths are secondary vessels. But that just isn’t how evolution works. Evolution does not have a trajectory—humans may love to regard themselves as occupying the pinnacle of life, but I’d wager that just about any other creature on the planet (except, maybe, teacup yorkies or hamsters) would beg to differ. The best way to counter this misconception with your students is to show them diagrams like the one here from UCMP.
Remind them that nodes can rotate! If you have 15 minutes, you can have students make their own manipulable evolutionary tree with pipe cleaners so they can actually rotate nodes themselves! And take every opportunity to remind them that any living organism—be it bacterium, fungus, or ape—is 100% equally “evolved.” Remind them that sea cucumbers can spew out their guts and run away! (And to answer your next question, no, I will never ever stop talking about gut-spewing sea cucumbers. Holothuroidea FTW!)
Misconception: The closer two organisms are on an evolutionary tree, the more closely related they are.
Correction: The more recently two organisms share a common ancestor, the more closely related they are.
You can’t draw any conclusions from the left-right positions of organisms in an evolutionary tree. (And why is that? Say it loud; say it proud: nodes can rotate!) The only way to figure out how closely two taxa (organisms or groups of organisms) are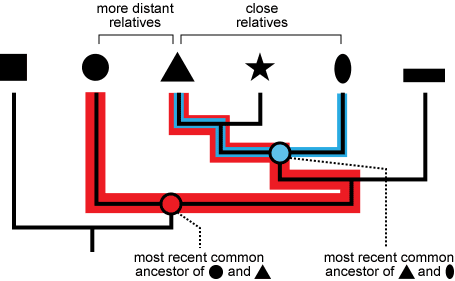 
related is to trace their ancestry back until you hit their common ancestor. So in the tree to the right, the circle and triangle are close together, but they are more distantly related than the triangle and the oval. Why? Because the common ancestor of triangle and oval lived more recently than the common ancestor of circle and triangle. Remember that time runs from root to tips on evolutionary trees, so the further back toward the root you have to go to get to the common ancestor of two taxa, the further back in time that ancestor lived. The further back in time the common ancestor, the longer the two taxa have been evolving independently, and therefore the more distantly related the taxa are.
How do you reinforce this idea with your students? Like this:
Pop Quiz!
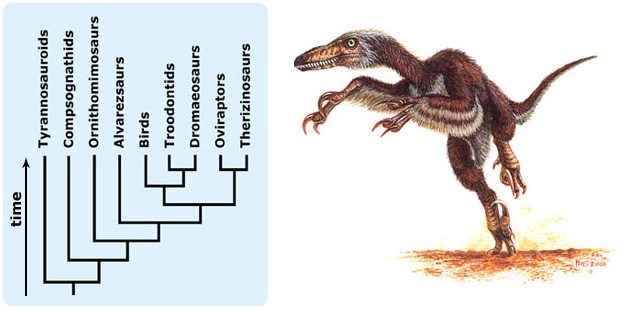
- Troodontids and oviraptors are both positioned equidistant from the dromaeosaurs on this tree. Is one of them more closely related to dromaeosaurs than the other? How do you know?
- Which group on this tree is most closely related to birds? (Hint: This is a trick question.)
- True or false: The producers of Jurassic World missed a golden opportunity to inspire a new generation of paleontologists by showing off all the cool things we have discovered in the last twenty years.
There is a chance that one of those questions has nothing to do with this misconception…
Misconception: The fewer nodes separating two taxa, the more closely related they are.
Correction: The more recently two organisms share a common ancestor, the more closely related they are.
Number of nodes might seem at first like a reasonable basis to judge relatedness. The more nodes you pass through along a lineage, the further back in time you’re going, right? But it doesn’t take long to realize that it just doesn’t work.
Remember that trees are models. The person constructing the tree can collapse and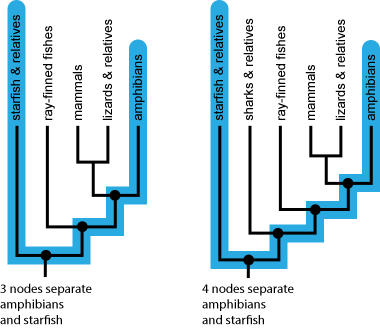 
expand the tree as needed, and even add and remove groups. And that affects the number of nodes between taxa. For example, here are two trees—one includes sharks and their relatives and the other doesn’t. So in the one tree, amphibians and starfish are separated by three nodes; but in the other, they are separated by four nodes. But, of course, how closely related these two groups are does not shift depending on the tree you’re looking at.
What if we compare number of nodes within the same tree? Does counting nodes to ascertain closeness of relation work then? Nope. Look at the tree here: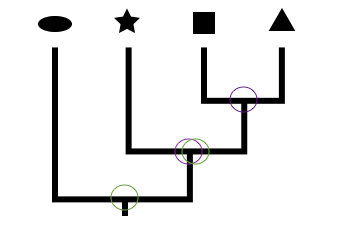 
How many nodes separate the oval and the star? Two (green circles). How many nodes separate the triangle and the star? Two (purple circles). But applying what we learned in the last misconception, we know that the star is more closely related to the triangle than the oval. In sum, the only way to judge relatedness is by determining how recently the taxa shared a common ancestor—there aren’t any shortcuts.
Are you enjoying your expedition into the wonderful world of tree-thinking? I hope so! There is more to come…
All images are courtesy University of California Museum of Paleontology's Understanding Evolution (http://evolution.berkeley.edu).
Are you a teacher and want to tell us about an amazing free resource? Do you have an idea for a future Misconception Monday or other post? See some good or bad examples of science communication lately? Drop me an email or shoot me a tweet @keeps3.
